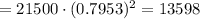Answer:
a)
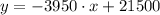
b) f(x)
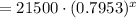
c) Year 1: Linear $17550, exponential $17099
Year 4: Linear $5700, exponential $8601
d) Exponential model
e) The linear model depreciates the value quicker than exponential model long term around 4 years
Explanation:
a) At year 0 the price is 21500 and at year 2 the price is 13600
WE can use points (0,21500) and (2,13600)
We can determine the gradient

We can use the point slow formula:
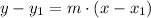

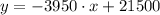
b) We can use the following equation:
f(x)
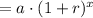
f(x) is the depreciation value after amount of time t, a is the new value, r is the rate of depreciation and x is the time.
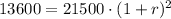

The depreciation rate is 20.47% and is negative because it decreases the new value of the car
c) Year 1:
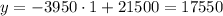
f(x)
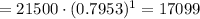
Year 4:
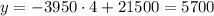
f(x)
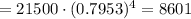
d) Year 2
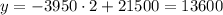
f(x)