Answer:
\k = -0.05017.:36 days
Explanation:
Given that The management of a factory finds that the maximum number of units a worker can produc in a day is 30. The learning curve for the number of units N produced per day after a new employee has worked for t days is modeled by
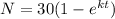
t = no of days
When t =20, we have N =19
Substitute to get
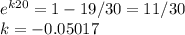
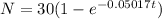
For producing 25 units per day, substitute N =25 and solve for t

t=35.71
i.e approximately 36 days should pass