Question

Population Growth

The number of a certain type of bacteria increases continuously at a rate proportional to the number present. There are 150 bacteria at a given time and 450 bacteria 5 hours later.
(a) How many bacteria will there be 10 hours after the initial time?
(b) How long will it take for the population to double?
(c) Does the answer to part (b) depend on the starting time? Explain your reasoning.

Answer 1

Explanation:

Given that the number of a certain type of bacteria increases continuously at a rate proportional to the number present.

Initial population = 150

Hence equation for population P would be

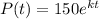`P(t) = 150e^(kt)` where t = time in hours

When t=5, P = 450

Substitute to get

`3 = e^(5k)`

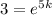
k=0.2197

`P(t) = 150e^(0.2197t)` is P(t)

P will double when

`300 = 150e^(0.2197t)`

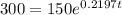
t =3.155

Between 3rd and 4th it would double

c) Yes it doubles when 3.155 hours lapsed from the start time since t in the equation is time lapsed from start time.