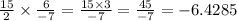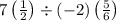 =
=
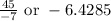
Explanation:
Given expression:
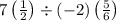
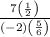
The fraction
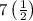 can be written by multiplying 7 with 2 and add to ‘1’. So,
can be written by multiplying 7 with 2 and add to ‘1’. So,
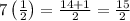
The fraction
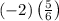 can be written by multiplying (-2) with 6 and add to ‘5’. So,
can be written by multiplying (-2) with 6 and add to ‘5’. So,
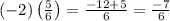
Applying these, we get
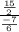
When do solving with numerator fraction, the denominator fraction
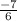 can be written as
can be written as
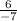 . Therefore,
. Therefore,