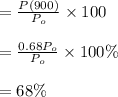Question

Radioactive Decay

what percent of a present amount of radioactive radium (226Ra) will remain after 900 years?

Answer 1

Percentage of (226Ra) after 900 years is 68%

Explanation:

Let P(t) be the amount of (226Ra) present at any time t

Half life of (226 Ra) = 1599 years

If P₀ is initial amount of (226 Ra) then after 1599 years

P(1599)=P₀/2

Decay i amount of radioactive substance is related to time t as

`(dP)/(dt)=kP(t)\\\\(1)/(P)\,dP=kdt\\\\Integrating\,\, both\,\,sides\\\\ln|P|=kt+c\\\\P(t)=Ce^(kt)\\\\at \,\, t=0\,\, P(0)=P_(o)\\\\P(0)=Ce^(k0)\\\\P_(o)=C\\\\then\\\\P(t)=P_(o)e^(kt)`

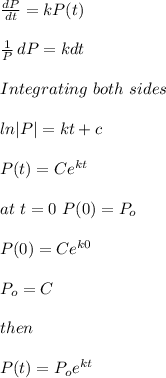
To find value of k

`at\,\, t=1599\,years\\\\P(1599)=(P_(o))/(2)\\\\then\\\\(P_(o))/(2) =P_(o)e^(k(1599))\\\\(1)/(2) =e^(k(1599))\\\\ln|(1)/(2)|=k(1599)\\\\k=(ln|(1)/(2)|)/(1599)=-4.3* 10^(-3)\\\\\implies P(t)=P_(o)e^{-4.3* 10^(-3)t}\\\\at\,\, t=900 \\\\P(900)=P_(o)e^{-4.3* 10^(-3)(900)}\\\\P(900)=0.68P_(o)`

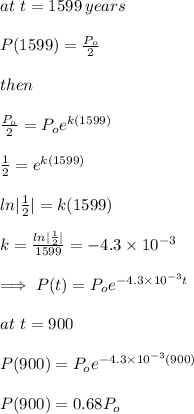
Percentage of radioactive element is:

Amount after 900 years
`=(P(900))/(P_(o))* 100\\\\=(0.68P_(o))/(P_(o))* 100\%\\\\=68\%`