Question

Radioactive Decay

Find the half-life of a radioactive material for which 99.57% of the initial amount remains after 1 year.

Answer 1

t=160.82 years

Explanation:

exponential decay function is

`A= A_1 e^(kt)`

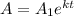
If initial amount A_1 is 100 then material remaining is 99.57

`99.57=100e^(kt)`

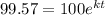
divide both sides by 100, question says 1 year so t=1

`.9957=e^(k(1))`

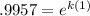
take ln on both sides

`ln(.9957)=k`

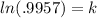
k=-.00431

`A=100e^(-.00431t)`

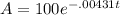
t=1, A= 50 remaining (half life)

`50=100e^(-.00431(t))`

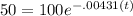
divide both sides by 100

`0.5=e^(-.00431t)`

take ln on both sides

t=160.82 years