Answer:
The eigenvector of A is not equal to zero, then we can say λ
 or λ = 0. Therefore, the only possible eigenvalues of A are 0.
or λ = 0. Therefore, the only possible eigenvalues of A are 0.
Explanation:
If we assume that λ is the eigenvalue of the matrix A and the eigenvector of the matrix A is ⁻ˣ. Therefore:
For
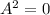
we have:
⁻0 = [⁰₀⁰₀][⁻ˣ] =
 *[⁻ˣ] = Aλ[⁻ˣ] = λ
*[⁻ˣ] = Aλ[⁻ˣ] = λ
 [⁻ˣ]
[⁻ˣ]
In the expression above, ⁻ˣ is not equal to zero, then λ
 = 0 or λ is = 0. This shows that the only possible eigenvalues of A are zero '0'
= 0 or λ is = 0. This shows that the only possible eigenvalues of A are zero '0'