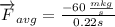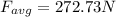Question

A 10 kg ball strikes a wall with a velocity of 3 m/s to the left. The ball bounces off with a velocity of 3 m/s to the right. If the ball is in contact with the wall for 0.22 s. What is the constant force (in newtons) exerted on the ball by the wall during the impact? Report your answer as a positive number.

Answer 1

The force is 272.73 newtons

Step-by-step explanation:

We're going to use impulse-momentum theorem that states impulse is the change on the linear momentum this is:

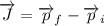`\overrightarrow{J}=\overrightarrow{p}_(f)-\overrightarrow{p}_(i)` (1)

Impulse is also defined as average force times the time the force is applied:

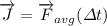`\overrightarrow{J}=\overrightarrow{F}_(avg)(\varDelta t)` (2)

By (2) on (1):

`\overrightarrow{F}_(avg)(\varDelta t)= \overrightarrow{p}_(f)-\overrightarrow{p}_(i)`

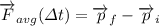
solving for
`\overrightarrow{F}_(avg)`:

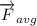`\overrightarrow{F}_(avg)=\frac{\overrightarrow{p}_(f)-\overrightarrow{p}_(i)}{\varDelta t}` (3)

We already know Δt is equal to 0.22 s, all we should do now is to find
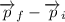`\overrightarrow{p}_(f)-\overrightarrow{p}_(i)` and put on (3) (
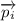`\overrightarrow{p_(i)}` the initial momentum and
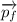`\overrightarrow{p_(f)}` the final momentum). Linear momentum is defined as
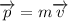`\overrightarrow{p}=m\overrightarrow{v}` , using that on (3):

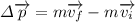`\varDelta\overrightarrow{p}=m \overrightarrow{v_(f)}-m \overrightarrow{v_(i)}` (4)

Velocity (v) are vectors so direction matters, if positive direction is the right direction and negative direction left
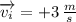`\overrightarrow{v_(i)}=+3\, (m)/(s)` and
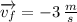`\overrightarrow{v_(f)}=-3\, (m)/(s)` so (4) becomes:

`\varDelta\overrightarrow{p}=m(-3(m)/(s)- (+3(m)/(s)))=-(10kg)(6(m)/(s))`

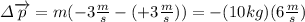
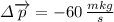`\varDelta\overrightarrow{p}=-60\, (mkg)/(s)` (5)

Using (5) on (3):

`\overrightarrow{F}_(avg)=(-60\, (mkg)/(s))/(0.22s)`

`F_(avg)=272.73N`