Question

Determining Exponential Growth and Decay in Exercise, use the given information to write an exponential equation for y. Does the function represent exponential growth or exponential decay?

dy/dt = -4y, y = 30 when t = 0

Answer 1

Answer:

`y=30e^(-4t)`

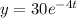
Exponential decay.

Explanation:

We are given that

`(dy)/(dt)=-4y`

y=30 when t=0

Taking integration on both sides then we get

`\int (dy)/(y)=-4\int dt`

`lny=-4t+C`

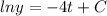
By using the formula
`\int (dx)/(x)=ln x,\int dx=x`

`y=e^(-4t+C)`

`y=e^(C)e^(-4t)=Ce^(-4t)`

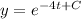
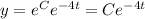
Where
`e^C=Constant=C`

`y=Ce^(-4t)`

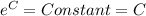
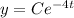
Substitute y=30 and t=0

`30=C`

`y=30e^(-4t)`

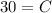
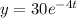
Apply limit t tends to infinity

`\lim_(t\rightarrow \infty)=\lim_(t\rightarrow\infty)30e^(-4t)=0`

The value of function decreases with time therefore, it is an exponential decay.