Answer:
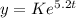
Exponential growth
Explanation:
We can solve this differential equation by the separation of variables method.
We have that:
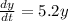
So
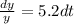
Integrating both sides
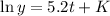
In which K is the value of y when t = 0.
We apply the exponential to both sides, so:
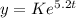
This is our exponential equation. Since the power of e is a positive value, the function represents exponential growth.