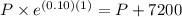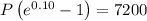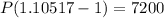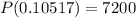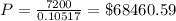a. An asset that generates $7200 yearly income if the interest rate 5% compounded continuously, then its capital value is $140433.002
b. An asset that generates $7200 yearly income if the interest rate 10% compounded continuously, then its capital value is $68460.59
Explanation:
For continuously compound interest
 ---------------> eq.1
---------------> eq.1
Where
P = principal amount (initial investment)
r = annual interest rate (as a decimal)
t = number of years
A = amount after time t.
Let’s solve the equation
Where,
P is unknown
A = P + 7200 (asset after 1 year) ---------------> eq. 2
Case A:

t = 1 (1 year)
Substitute all values in the formula (2) using the formula (1),

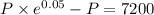
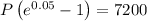
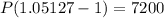
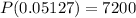
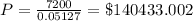
Case B:
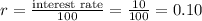
t = 1 (1 year)
Substitute all values in the formula (2) using the formula (1),