Question

Researchers are interested in the effect of a certain nutrient on the growth rate of plant seedlings. Using a hydroponics grow procedure that utilized water containing the nutrient, they planted six tomato plants and recorded the heights of each plant 14 days after germination. Those heights, measured in millimeters, were as follows: 53.1, 60.2, 60.6, 62.1, 64.4, 68.6.

1. What is the point estimate of the population mean height of this variety of seedling 14 days after germination? Do not round your final answer.

2. Given a margin of error of 5.4 mm, construct a 95% confidence interval for the population mean height. Enter only the lower limit for your confidence interval rounded to one decimal place.

3.Given a margin of error of 5.4 mm, construct a 95% confidence interval for the population mean height. Enter only the upper limit for your confidence interval rounded to one decimal place.

4. Why is a point estimate alone usually insufficient for statistical inference?

A. A point estimate alone is insufficient because the sampling distribution is not centered at the parameter.
B. An interval estimate gives us a sense of the accuracy of the point estimate whereas a point estimate alone does not.
C. The point estimate usually falls outside the confidence interval.
D.The point estimate has a large standard deviation compared to other estimators.

Answer 1

1. the point estimate:mean =61.5 mm

standard deviation = 5.143 mm

2. the lower limit of the confidence interval =50.9 mm

3. the upper limit of the confidence interval =72.1 mm

4. B. An interval estimate gives us a sense of the accuracy of the point estimate whereas a point estimate alone does not.

Explanation:

1. An estimate of a population parameter,such as mean or standard deviation, based on a single number is called a point estimate.

for this question; the point estimate of the mean and standard deviation of the height of 6 samples are calculated

mean = (53.1 + 60.2+ 60.6+ 62.1+ 64.4+68.6.)/6 = 369/6 = 61.5 mm

standard deviation = 5.143 mm

variance = 26.45

2. margin of error, σₓ of 5.4 mm

confidence interval of 95% gives a Zc of 1.96 from the table of confidence coefficient

confidence interval, µ =

µ= x ±zc σx = 61.5 ± 1.96*5.4 = 61.5 ± 10.584

the lower limit of the confidence interval =50.9 mm

3. the upper limit of the confidence interval =72.1 mm

4.

a point estimate alone usually insufficient for statistical inference

B. An interval estimate gives us a sense of the accuracy of the point estimate whereas a point estimate alone does not.

Answer 2

1) The mean calculated for this case is
`\bar X=61.5`

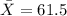
2)
`61.5-5.4=56.1`

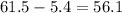
3)
`61.5+5.4=66.9`

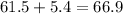
4) B. An interval estimate gives us a sense of the accuracy of the point estimate whereas a point estimate alone does not.

Because with the confidence interval we know the confidence level of the interval, and the limits for the parameter at some significance level.

Explanation:

Previous concepts

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

Part 1

In order to calculate the mean and the sample deviation we can use the following formulas:

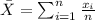`\bar X= \sum_(i=1)^n (x_i)/(n)` (a)

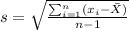`s=\sqrt{(\sum_(i=1)^n (x_i-\bar X))/(n-1)}` (b)

The mean calculated for this case is
`\bar X=61.5`

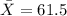
The sample deviation calculated
`s=5.143`

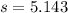
`\mu` population mean (variable of interest)

n=6 represent the sample size

Part 2

The confidence interval for the mean is given by the following formula:

`\bar X \pm ME` (1)

So if we have the margin of error 5.4mm we can find the lowr limit like this:

`61.5-5.4=56.1`

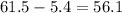
Part 3

`61.5+5.4=66.9`

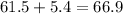
Part 4

B. An interval estimate gives us a sense of the accuracy of the point estimate whereas a point estimate alone does not.

Because with the confidence interval we know the confidence level of the interval, and the limits for the parameter at some significance level.