Answer:
a)
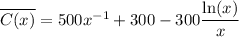
b)
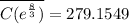
Explanation:
Given the cost function as C(x):
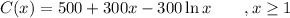
a) Find the average cost function,

if C is the cost of selling x units, The Average can be denoted by:
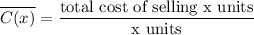
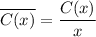
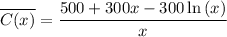
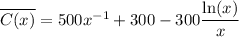
this is the average cost function
b) The minimum average cost:
To find the minimum average cost, we'll have to differentiate the average cost function
 . and equate it to zero. (like finding the stationary point of any function)
. and equate it to zero. (like finding the stationary point of any function)
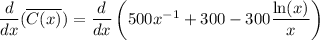
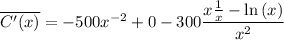
now just simplify:
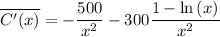
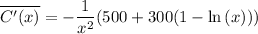
we've found the derivative of C(x), now to find the minimum we'll equate this derivative to zero.
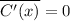

and now solve for x
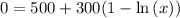
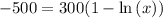
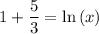

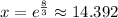
at this value of x the average cost is minimum.
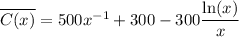
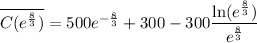
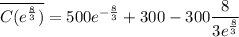
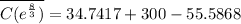
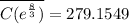
This is the minimum average cost!