Question

Analyzing a Graph In Exercise, analyze and sketch the graph of the function. Lable any relative extrema, points of inflection, and asymptotes. See Example 6.

y = (ln x)2

Answer 1

`y=(ln(x))^2`

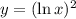
point of extremity: (1,0)

vertical asymptote: along the y-axis (x = 0)

point of inflection: (e,1)

Solution:

Although all these points can be directly observed from the graph below, but these are the analytical solutions if you're curious!

1) Extreme point can be found by differentiating 'y' once and equating to zero. solving for x:

`(dy)/(dx)=(dy)/(dx)((ln(x))^2)`

`(dy)/(dx)=2ln(x)\left((1)/(x)\right)`

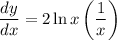
substitute dy/dx = 0, and solve for x

`0=2ln(x)\left((1)/(x)\right)`

`0=2ln(x)`

`x=e^0`

`x=1`

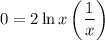
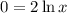
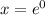
use this value of x back in y, to find the y-coordinate of the extreme point

`y=(ln(1))^2`

`y=0`

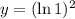
The extreme point = (1,0)

2) Differentiate y twice to find the inflection point.

`(dy)/(dx)=2ln(x)\left((1)/(x)\right)`

`(d^2y)/(dx^2)=2ln(x)\left(-(1)/(x^2)\right)+\left((1)/(x)\right)\left((2)/(x)\right)`

`(d^2y)/(dx^2)=(2)/(x^2)\left(-ln(x)+1}\right)`

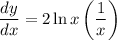
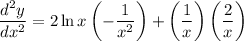
substitute d2y/dx2 = 0, and solve for x

`0=(2)/(x^2)\left(-ln(x)+1}\right)`

`0=-ln(x)+1`

`ln(x)=1`

`x = e`

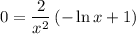
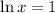
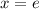
use this value of x back in y, to find the y-coordinate of the inflection point

`y=(ln(e))^2`

`y=1`

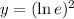
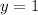
The extreme point = (e,1)