Answer:
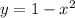
Explanation:
we're given three points (0,1),(1,0) and (-1,0). and and equation of a parabola
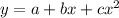
we can plug in each of the coordinates, and 3 equations
(x,y) = (0,1)
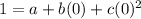

(x,y) = (1,0)
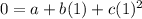
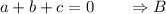
(x,y) = (-1,0)
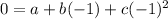
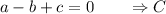
These are are three equations, well we can simultaneously solve them to find the values of a, b and c.
we already found that, a = 1. so we plug this value in the rest of the equations. we'll use equation B.
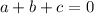
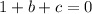
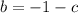
we can substitute this value of b and a = 1, equation C
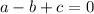
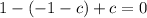
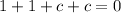
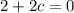
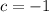
we can use this value of c back in b
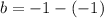
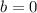
hence our equation of the 2-degree polynomial will be:
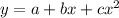
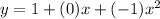
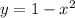
and this polynomial indeed passes through all the points (0, 1), (1, 0), and (-1, 0).
And since these are the only solutions to the simultaneous equation we solved (i.e. we have single values of a,b and c). there's no other possibility.