Answer:
Analyzed and Sketched.
Explanation:
We are given
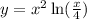 .
.
For sketching graph, we need to determine the following.
1) First derivative of y with respect to x to determine the interval where function increases and decreases.
2) Second derivative of y with respect to x to determine the interval where function is concave up and concave down.
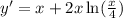
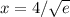 is absolute minimum.
is absolute minimum.
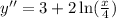
 is point where concavity changes from down to up.
is point where concavity changes from down to up.
Since it is logarithmic function, the graph covers right side of the x-axis and it cannot take the value pair (0,0)
The sketch is in attachment.