Question

A. Use your calculator to approximate ∫^ b_0 e^-0.00001x dx for b=10, 50, 100 and 1000.

b. Based on your answers to part a, does ∫^[infinity]_0 e^-0.00001 dx appear to be convergent or divergent?
c. To what value does the integral actually converge?

Answer 1

Explanation:

We are to integrate the function

`e^-0.00001x` from 0 to b for different ascending values of x.

`\int e^-0.00001x = -10^5 e^-0.00001x`

Now we substitute the limits

When b =10

I = integral value =
`-10^5 e^-0.00001*10`

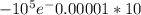
b =50, I =
`-10^5(e^-0.00001*50-1)`

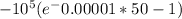
b =100, I =
`-10^5( e^-0.00001*100-1)`

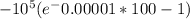
b =1000 I=
`-10^5 (e^-0.00001*1000-1)`

b) As b increases exponent increases in negative, or denominator increases hence when b becomes large this will be a decreasing sequence hence converges

c) Converges to
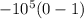`-10^5 (0-1)`=10^5