Question

Analyzing a Graph In Exercise, analyze and sketch the graph of the function. Lable any relative extrema, points of inflection, and asymptotes. See Example 6.

y = ln 2x - 2x2

Answer 1

Analyzed and Sketched.

Explanation:

We are given
`y = \ln(2x) - 2x^2`.

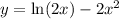We need to find the following to sketch the graph.

1) First derivative of y with respect to x to determine the interval where function increases and decreases.

2) Second derivative of y with respect to x to determine the interval where function is concave up and concave down.

`y' = (1)/(x) - 4 x=0`

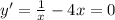
The roots are x = -1/2 and x = 1/2 but negative one cannot be possible due to logarithmic function.

x = 1/2 is absolute maximum.

`y''=-4 - (1)/(x^2)`

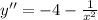
So, concavity is always down.

Here, x = 0 is vertical asymptote.

I attached the picture of sketched graph.