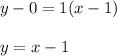Question

Finding an Equation of a Tangent Line In Exercise, use implicit differentiation to find an equation of the tangent line to the graph of the function at the given point.

x + y - 1 = ln(x2 + y2); (1, 0)

Answer 1

Equation of tangent line at point (1,0) to given function is

y=x-1

Explanation:

Equation of tangent line is

y-y₁=m(x-x₁)-----(1)

where m is slope of line and can be found by implicitly differentiating the given function w.r.to x

`x+y-1=ln(x^(2)+y^(2))\\\\(d)/(dx)(x+y-1)=(d)/(dx)(ln(x^(2)+y^(2))\\\\1+(dy)/(dx)=(2x)/(x^(2)+y^(2))+(2y)/(x^(2)+y^(2))(dy)/(dx)\\\\(dy)/(dx)=(2x-x^(2)-y^(2))/(x^(2)+y^(2)-2y)\\\\at \,(1,0)\\\\(dy)/(dx)=(2(1)-1-0)/(1+0-0)\\\\(dy)/(dx)=1\\\\`

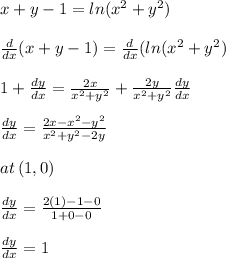
which is slope of tangent line. At (1,0) equation of tangent line is

`y-0=1(x-1)\\\\y=x-1`