Question

Show that
∫^[infinity]_1 1/x^p dx
converges if >1 and diverges if p≤1.

Answer 1

Explanation:

Consider the integral

`\int\limits^1_(-infty)  (1)/(x^p)  \, dx`

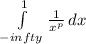
for various values of p

CaseI:p =1 Then integral is ln x and for infinity this value diverges so diverges

Case 2: p<1

The integrated value would be
`(x^(-p+1) )/(-p+1)`

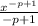
Since P <1 numerator x will have positive exponent and when infinity is substituted this will diverge

Case 3: p >1

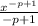`(x^(-p+1) )/(-p+1)` will have x with negative exponent. So when x = infinity this value becomes 0 thus making the integral to converge