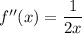Question

Finding Higher-Order Derivatives In Exercise, find the second derivative of the function.

f(x) = x ln (x)^1/2 + 2x

Answer 1

Answer: The second derivative of the function is
`f''(x)=(1)/(2x)`

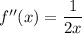
Explanation:

Since we have given that

`f(x)=x\ln √(x)+2x`

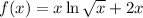
We need to find the second derivative of the function.

So, the first derivative would be

`f'(x)=1* \ln√(x)+x(1)/(√(x))* (1)/(2√(x))+2\\\\f'(x)=\ln √(x)+(1)/(2)+2\\\\f'(x)=\ln√(x)+(3)/(2)`

Now, second derivative would be

`f''(x)=(1)/(√(x))* (1)/(2√(x))\\\\f''(x)=(1)/(2x)`

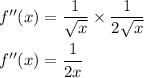
Hence, the second derivative of the function is
`f''(x)=(1)/(2x)`