Question

Finding an Equation of a Tangent Line In Exercise, find an equation of the tangent line to the graph of the function at the given point. See Example 5.

f(x) = ln{x(x + 3)^1/2}; (6/5, 9/10)

Answer 1

`75x-70y=27`

Explanation:

We are given that

`y=ln(x(x+3)^{(1)/(2)})`

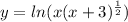
Point (
`(6)/(5),(9)/(10)`)

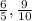We have to find the equation of tangent line to the given graph.

Differentiate w.r.t x

`(dy)/(dx)=\frac{1}{x(x+3)^{(1)/(2)}}* ((x+3)^{(1)/(2)+x* (1)/(2)(x+3)^{-(1)/(2)})`

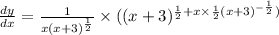
By using formula

`(d(lnx))/(dx)=(1)/(x)`

`(dx^n)/(dx)=nx^(n-1)`

`(d(u\cdot v))/(dx)=u'v+v'u`

`(dy)/(dx)=(x+3+x)/(x(x+3))=(2x+3)/(x(x+3))`

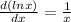
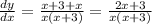
Substitute x=6/5

`m=(dy)/(dx)=((12)/(5)+3)/((6)/(5)((6)/(5)+3))=(15)/(14)`

`m=(dy)/(dx)=(15)/(14)`

Slope-point form:

`y-y_1=m(x-x_1)`

`x_1=6/5,y_1=9/10`

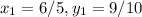
By using this formula

The equation of tangent to the given graph

`y-(9)/(10)=(15)/(14)(x-(6)/(5))`

`(10y-9)/(10)=(15)/(14)(x-(6)/(5))`

`140y-126=150x-180`

`150x-140y=180-126=54`

`75x-70y=27`

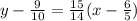
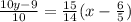
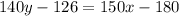
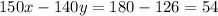
The equation of tangent to the given graph

`75x-70y=27`