Question

Select the function that defines the given sequence

-11, -8, -5,-2,-1,...

A. F(1)= -11
F(n) = f(n - 1) - 3; for n = 2,3,4,...

B. F(1) = -11
F(n) = f(n-1) + 3; for n = 2,3,4...

C. F(1) = -11
F(n) f(n+1) -3; for n = 2,3,4,...

D. F(1) = -11
F(n) = f(n+1) + 3; for n = 2,3,4...

Answer 1

b

Explanation:

Answer 2

B. F(1) = -11

F(n) = f(n-1) + 3; for n = 2,3,4...

Explanation:

The given sequence is -11, -8, -5,-2,-1,...

The first term is f(1)=-8 and the common difference is

`d = - 8 - - 11 = 3`

The recursive definition of this sequence is given by:

`f(n) = f(n - 1) + d`

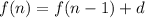
This implies that:

`f(n) = f(n - 1) +3 \: where \: f(1) = - 11`

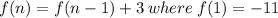
and n=2,3,4,5,...

The second choice is correct