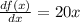Answer:
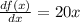
Explanation:
to find the derivative of the function
 we use the chain rule approach. which simply involves increasing x by Δx and carrying out simple arithmetic operation.
we use the chain rule approach. which simply involves increasing x by Δx and carrying out simple arithmetic operation.
The First step is to increase x by Δx

increase x by Δx and and f(x) by Δf(x)

if we expand we have
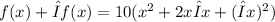
if we expand we have
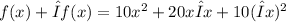
next we subtract f(x) from both sides


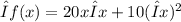
Next we divide all through by Δx

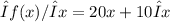
next we let the limit of Δx tends zero, we arrive at
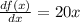
hence the derivative of the function
 is
is