Question

Find
∫^[infinity]_-[infinity] xe^-x^2 dx.

Answer 1

Zero

Explanation:

We are to find

`\int\limits^(infinity) _(-infinity) xe^-x^2 dx.`

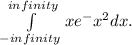
Here the integral is of the form x varying from negative to positive

And negative limit = positive limit in dimension

Let us assume
`f(x) =xe^(-x^2)`

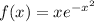
A function is odd if f(x) = -f(-x) and even if f(x) = f(-x)

Let us check f(-x) = -f(x)

So f is an odd function.

As per properties of integration, we have

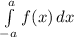`\int\limits^a_(-a)  {f(x)} \, dx`=0 if fis an odd function.

Our function f is odd and a = infinity

So we can apply this rule to find out the

integral value is zero.