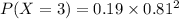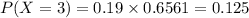Question

Assume that a procedure yields a geometric distribution where the probability of success is 19%. Use the geometric probability formula to find the probability that the first success occurs on the third trial.

A)0.469

B)0.207

C)0.125

D)0.544

Answer 1

The probability that the first success occurs on the third trial is 0.125.

Answer: Option C

Explanation:

The probability of success is given by the geometric distribution formula:

`P(X=x)=p * q^(x-1)`

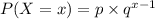
Where,

p = probability of success for single trial.

q = probability of failure for a single trial (1-p)

x = the number of failures before a success.

P(X = x) = Probability of x successes in n trials.

Given:

p = 19% = 0.19

q = 1 – p = 1 – 0.19 = 0.81

x = 3

We want to find the probability that the first success occurs on the third trial so,

`P(X=3)=0.19 * 0.81^((3-1))`

`P(X=3)=0.19 * 0.81^(2)`

`P(X=3)=0.19 * 0.6561=0.125`