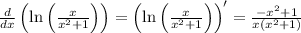Answer:
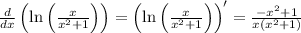
Explanation:
To find the derivative of the function
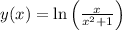 you must:
you must:
Step 1. Rewrite the logarithm:
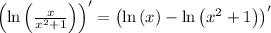
Step 2. The derivative of a sum is the sum of derivatives:
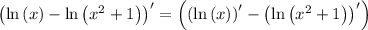
Step 3. The derivative of natural logarithm is
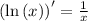
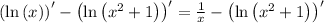
Step 4. The function
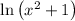 is the composition
is the composition
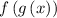 of two functions
of two functions
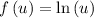 and
and
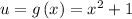
Step 5. Apply the chain rule
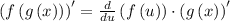
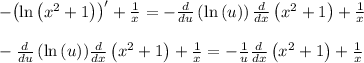
Return to the old variable:
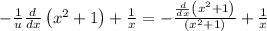
The derivative of a sum is the sum of derivatives:
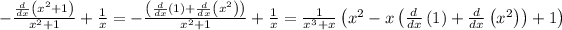
Step 6. Apply the power rule
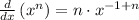
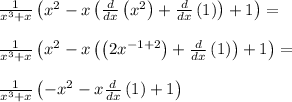
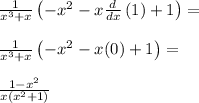
Thus,