Question

Answer the following questions in a Word document and upload the document to the appropriate drop box.1) Using the chart, approximate the limit of the function f(x) = sin x/ x as x approaches zero. Note the numbers are in radians: x-1-0.25-0.01-0.0050.0050.010.251f(x)0.01750.98960.9999…0.9999…0.9999…0.9999…0.98960.0175Round the values for f(x) to 4 places2) Using a method like 1 above, approximate the limit of the function f(x) = (1 + x)(1/x)as x approaches zero to three decimal places. What famous number does this limit approach?

Answer 1

Before answering the question I must clarify that I believe the second function must be:
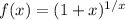`f(x)=(1+x)^(1/x)` since the function f(x)=(1+x)(1/x) doesn't quite return a famous number.

Answer:

1)
`\lim_(x \to 0) (sin x)/(x)=1`

2)
`\lim_(x \to 0) (1+x)^(1/x)=2.725` This limit approaches the famous euler's number e.

Explanation:

Iin order to solve this problem we must fill the table. The table is filled by calculating each x-value for the given function, for example, for the first function and the first value we get that:

`f(x)=(sin x)/(x)`

`f(-1)=(sin (-1))/(-1)=0.84147098`

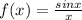
likewise for the second value we get that:

`f(-0.25)=(sin (-0.25))/(-0.25)=0.98961584`

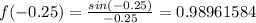
and so on, likewise with the second function:

`f(x)=(1+x)^(1/x)`

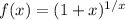
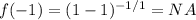`f(-1)=(1-1)^(-1/1)=NA` this is because this function yields a division into zero which is not defined for the real numbers.

`f(-0.25)=(1-0.25)^(-1/0.25)=2.731999026`

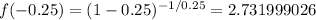
and so on. In the attached picture I included the completed table.

Since we are interested in the limit as x approaches zero, we need to look at the x-values that are closest to zero. In this table it's the values that are colored yellow. As you can see in the first function's column, the limit as x approaches zero of the first function approximates to 1, so:

1)
`\lim_(x \to 0) (sin x)/(x)=1`

In the second function, we can see that the limit as x approaches to zero is 2.725, so:

2)
`\lim_(x \to 0) (1+x)^(1/x)=2.725` This limit approaches the famous euler's number e.

Euler's number is a constant with a value of e=2.718281828

which as you may see is pretty close to the number found in the table. Of course, the closest we get to zero, the closest we will get to the actual value of euler's number, for example, if we used x=0.00000001, that would yield an answer of: 2.7183 which as you may see is closer to euler's number.