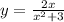Answer:
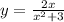
Explanation:
The derivative of an addition/subtraction of terms is the addition/subtraction of the derivatives of these terms.
The derivative of a constant is 0.
The derivative of
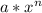 is
is
 . The derivative of
. The derivative of
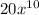 is
is
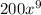 , for example.
, for example.
The derivative of the ln function:
If we have:

The derivative is
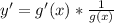
In this problem, we have that:
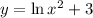
So
 and
and
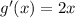
So the derivative to this function is