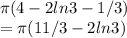Answer:
Explanation:
Here we have the curve xy =6 bounded by the line y=2, y=6 and x=6.
This region is rotated about x =6
We have to find the volume
Since rotated about vertical line parallel to y axis, shifting y axis to right by 6 units we get
the curve equation as
(6-x)y=6
6y-6xy =6
6xy =6(y-1)
x = (y-1)/y
and limits for y is 2 to y
Volume =
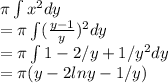
Substitute limits
Volume =