Answer:
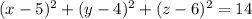 .
.
(Expand to obtain an equivalent expression for the sphere:
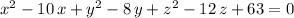 )
)
Explanation:
Apply the Pythagorean Theorem to find the distance between these two endpoints:
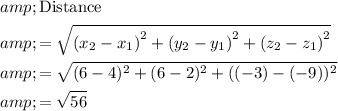 .
.
Since the two endpoints form a diameter of the sphere, the distance between them would be equal to the diameter of the sphere. The radius of a sphere is one-half of its diameter. In this case, that would be equal to:
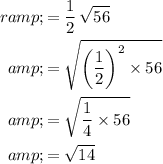 .
.
In a sphere, the midpoint of every diameter would be the center of the sphere. Each component of the midpoint of a segment (such as the diameter in this question) is equal to the arithmetic mean of that component of the two endpoints. In other words, the midpoint of a segment between
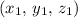 and
and
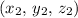 would be:
would be:
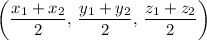 .
.
In this case, the midpoint of the diameter, which is the same as the center of the sphere, would be at:
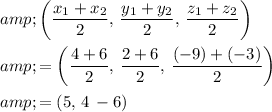 .
.
The equation for a sphere of radius
 and center
and center
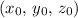 would be:
would be:
 .
.
In this case, the equation would be:
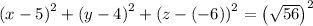 .
.
Simplify to obtain:
 .
.
Expand the squares and simplify to obtain:
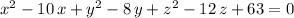 .
.