Question

20 points
For the function f defined by f(x)=3x2−2x−12 find f(−x) , −f(x) and −f(−x).

Answer 1

`f(-x) = 3x^2+2x - 12`

`-f(x) = -3x^2+2x+12`

`-f(-x) = -3x^2-2x+12`

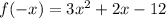
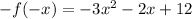
Solution:

Given function is:

`f(x) = 3x^2-2x-12`

We have to find f( - x) and -f(x) and -f(-x)

Let us first find f(-x)

Substitute x = -x in given function

`f(-x) = 3(-x)^2-2(-x)-12\\\\f(-x) = 3x^2+2x - 12`

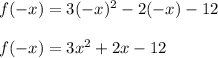
Thus f(-x) is found

Now find the value of -f(-x)

Multiply the above found f(-x) by -1

`-f(-x) = -1 * f(-x)\\\\-f(-x) = -1 * (3x^2+2x - 12)\\\\-f(-x) = -3x^2-2x+12`

Thus -f(-x) is found

Now find the value of -f(x)

Multiply the given function f(x) by -1

`-f(x) = -1 * f(x)\\\\-f(x) = -1 * (3x^2-2x-12)\\\\-f(x) = -3x^2+2x+12`

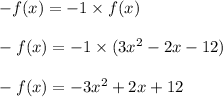
Thus -f(x) is found