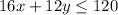 is the inequality that represents this situation
is the inequality that represents this situation
The greatest number of large dogs that she could have walked that afternoon is 3
Solution:
Each afternoon maria walks the dogs at a local pet shelter for up to 2 hours
Maria spends 16 minutes walking a large dog and 12 minutes walking a small dog
To find: Inequality for this situation
Let "x" be the number of large dogs taken for walking
Let "y" be the number of small dogs taken for walking
Total time spend = 2 hours = 120 minutes
Time spent for large dog = 16 minutes
Time spent for small dog = 12 minutes
Therefore, a inequality is framed as:
number of large dog x Time spent for large dog + number of small dogs x Time spent for small dog
 Total time spend
Total time spend
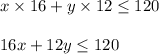
Here we used "less than or equal to" , since total time spend is up to 2 hours
Thus the inequality is found
If maria walked 9 dogs in one afternoon, what is the greatest number of large dogs that she could have walked that afternoon?
So total dogs = 9
number of large dogs + number of small dogs = 9
x + y = 9
y = 9 - x --- eqn 1
Substitute eqn 1 into inequality
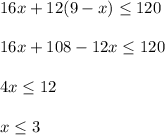
Thus the greatest number of large dogs that she could have walked that afternoon is 3