Answer:
10, 12, 14, 16
Explanation:
Given: Four consecutive even integers such that seven times the first exceeds their sum by 18.
Lets assume the first number be "x".
As it is even integers
∴ Second consecutive number will be
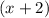
Third consecutive number will be
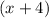
Fourth consecutive number will be
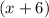
Now, as given seven times the first exceeds their sum by 18.
∴
![[x+(x+2)+(x+4)+(x+6)]+18 = 7x](https://img.qammunity.org/2021/formulas/mathematics/middle-school/o9qyvow7barl1xzcgpozys2s2qi0cvib3u.png)
solving the equation to find the number.
⇒
![[x+(x+2)+(x+4)+(x+6)]+18 = 7x](https://img.qammunity.org/2021/formulas/mathematics/middle-school/o9qyvow7barl1xzcgpozys2s2qi0cvib3u.png)
Opening parenthesis
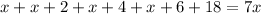
⇒

subtracting both side by 4x
⇒
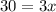
Dividing both side by 3
∴ x= 10.
Hence, subtituting the value x to find four consecutive even integers.
First number is 10
Second consecutive number will be
 = 12
= 12
Third consecutive number will be
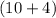 = 14
= 14
Fourth consecutive number will be
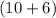 = 16
= 16
∴ Four consecutive even integers are 10,12,14,16.