Question

The notation Ak meas the matrix A Multiplied with itself k times (a) For the 2×2 identity matrix I, show that I2 =I (b)For the n×n identity matrix I, show that I2 =I (c) what do you think the enteries of Ik are?

Answer 1

Entries of I^k are are also identity elements.

Explanation:

a) For the 2×2 identity matrix I, show that I² =I

`I^(2)=\left[\begin{array}{cc}1&0\\0&1\end{array}\right] * \left[\begin{array}{cc}1&0\\0&1\end{array}\right] \\\\=\left[\begin{array}{cc}1* 1+0* 0&1* 0+0* 1\\0* 1+1* 0&0* 0+1*1\end{array}\right] \\\\=\left[\begin{array}{cc}1&0\\0&1\end{array}\right]`

Hence proved I² =I

b) For the n×n identity matrix I, show that I² =I

n×n identity matrix is as shown in figure

Elements of identity matrix are

`\delta I_(ij)=1\quad if\quad i=j\\\delta I_(ij)=0\quad if\quad i\\e j\\`

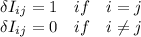
As square of 1 is equal to 1 so for n×n identity matrix I, I² =I

(c) what do you think the enteries of Ik are?

As mentioned above

`\delta I_(ij)=1\quad if\quad i=j\\\delta I_(ij)=0\quad if\quad i\\e j\\`

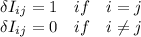
Any power of 1 is equal to 1 so kth power of 1 is also 1. According to this Ik=I