Answer:
Applying Quotient and power rule. Graphically, for x>0 both curves coincide.
Explanation:
1) Firstly, by applying the Quotient and then the Power Rule, we have a subtraction of the argument and, finally the exponent turns to be the coefficient. As it follows:
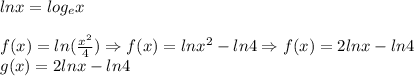
2) Check the graph below to see this equivalence. to see x>0 they both coincide.