Answer:
The solution tells me that in 124.5 years the value of the dollar in both investments will be the same
Explanation:
Let
t ----> the number of years
f(t) ---> the dollar value of one investment
g(t) ---> the dollar value of the other investment
we have
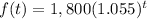
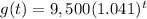
Solve the equation f(t)=g(t)
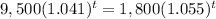
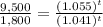
Rewrite
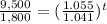
Apply log both sides
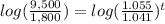
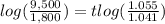
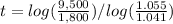
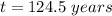
therefore
The solution tells me that in 124.5 years the value of the dollar in both investments will be the same