Question

Compound Interest A deposite of $1000 is made in an account that earns interest at an annual rate of 5%.How long will it take for the balance to double When the interest is compounded (a) annually,(b) monthly,(c) daily,and (d) continously?

Answer 1

(a) 14.21

(b) 13.78

(c) 13.57

(d) 13.86

Explanation:

Compound Interest, compounded n times per year,

`A = P(1 + (r)/(n) )^(nt)`

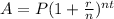
Compound Interest, compounded continuously,

`A = Pe^(rt)`

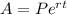
Where

A is the new amount/balance

P is the Principal (amount invested)

r is the rate in percentage

n is the number of times it is compounded.

Given:

Principal, P = $1000

rate, r = 5% = 0.05

For the balance to double, A = 2 × $1000

A = $2000

(a) annually, n = 1

`2000 = 1000(1 + (0.05)/(1) )^(1 * t)`

`2 = (1 + 0.05)^(t)`

`2 = (1.05)^(t)`

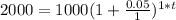
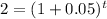
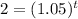
To solve for t, we take
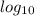`log_(10)` of both sides

`log_(10)2 = log_(10)1.05^(t)`

`log_(10)2 = t(log_(10)1.05)`

`t = (log_(10)2)/(log_(10)1.05)`

`t = (0.3010)/(0.0212)`

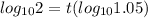
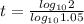
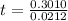
t = 14.21

(b) monthly, n = 12

`2000 = 1000(1 + (0.05)/(12) )^(12 * t)`

`2 = (1 + 0.0042)^(12t)`

`2 = (1.0042)^(12t)`

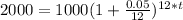
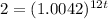
To solve for t, we take
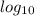`log_(10)` of both sides

`log_(10)2 = log_(10)1.0042^(12t)`

`log_(10)2 = 12t(log_(10)1.0042)`

`t = (log_(10)2)/(12 * log_(10)1.0042)`

`t = (0.3010)/(0.0218)`

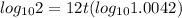
t = 13.78

(c) daily, n = 365

`2000 = 1000(1 + (0.05)/(365) )^(365 * t)`

`2 = (1 + 0.00014)^(365t)`

`2 = (1.00014)^(365t)`

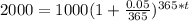
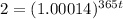
To solve for t, we take
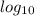`log_(10)` of both sides

`log_(10)2 = log_(10)1.00014^(365t)`

`log_(10)2 = 365t(log_(10)1.00014)`

`t = (log_(10)2)/(365 * log_(10)1.00014)`

`t = (0.3010)/(0.022)`

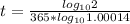
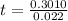
t = 13.565

t = 13.57

(d) Continuously

`2000 = 1000e^(0.05t)`

`2 = e^(0.05t)`

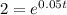
To solve for t, we take
`log_(e)` of both sides

`log_(e)2 = log_(e)e^(0.05t)`

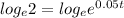
But log_{e}e = 1

In2 = 0.05t

`t =(In2)/(0.05)`

`t =(0.693)/(0.05)`

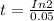
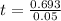
t = 13.86