Question

Determine the time required for a 16.00 gram sample of Ge-81 to decay until only 1.00 gram of the sample remains unchanged​

Answer 1

The time required for a 16.00 gram sample of Ge-81 to decay until only 1.00 gram of the sample remains unchanged

30.4 second

Step-by-step explanation:

Half-life = It is the time required by the radioactive substance to becomes half of its original value

For Ge

Half-life = 7.6 s

(it is experimentally determined value)

Calculate how many half-cycles are required to decay 16g of substance to 1 g

(For this divide the original quantity by 2 each time)

`16\rightarrow 8\rightarrow 4\rightarrow 2\rightarrow 1`

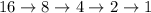
n = number of Half- cycles

Hence total n = 4

1 half - cycles = 7.6 s

4 half-cycles = 4 x 7.6

= 30.4 seconds

Second method :

This can also be calculated by using formula :

`N=N_(0)e^(-\lambda t)`

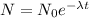
N = Amount of substance after decay

N0 = Original amount of the substance

t = Time required for decay

`\lambda` = decay constant

`\lambda =(0.693)/(Half-life)`

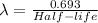
Half -life = 7.6 s

N = 1 g

N0 = 16 g

Insert the values in formula and then Calculate t