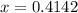Answer:
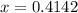
Explanation:
The first step to solve this equation is placing everything with the logarithmic to one side of the equality, and everything without the exponential to the other side. So
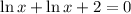
Now we have to write the left side as one ln only.
We have that
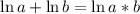
So
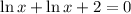
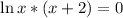
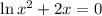
We have that the exponential and the ln are inverse functions. This means that
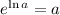 . So we apply the exponential to both sides of the equality
. So we apply the exponential to both sides of the equality
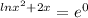
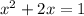
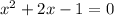
This is a quadratic equation, with roots -2.4142 and 0.4142. There is no ln for negative numbers, so the solution to this equation is: