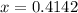Question

Solving Exponential and Logarithmic Equation In exercise,solve for x or t.See example 5 and 6.

In x + In(x + 2) = 0

Answer 1

`x = 0.4142`

Explanation:

The first step to solve this equation is placing everything with the logarithmic to one side of the equality, and everything without the exponential to the other side. So

`ln(x) + ln(x + 2) = 0`

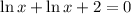
Now we have to write the left side as one ln only.

We have that

`ln(a) + ln(b) = ln(a*b)`

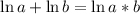
So

`ln(x) + ln(x + 2) = 0`

`ln(x*(x+2)) = 0`

`\ln{x^(2) + 2x} = 0`

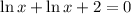
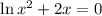
We have that the exponential and the ln are inverse functions. This means that
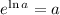`e^(ln(a)) = a`. So we apply the exponential to both sides of the equality

`\e^{ln{x^(2) + 2x}} = e^(0)`

`x^(2) + 2x = 1`

`x^(2) + 2x - 1 = 0`

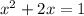
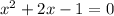
This is a quadratic equation, with roots -2.4142 and 0.4142. There is no ln for negative numbers, so the solution to this equation is:

`x = 0.4142`