Answer:
6 mph
Explanation:
Here is the complete question: Starting at home Nadia traveled uphill to the grocery store for 30 minutes at just 4mph. She then traveled back home along the same path downhill at a speed of 12 mph. What is her average speed for the entire trip from home to the grocery store and back?
Given: Time taken to travel uphill to the grocery store is 30 minutes.
Speed of travelling uphill to the grocery store is 4 mph.
Speed of travelling downhil to the home is 12mph.
First converting the unit if time given:
Time taken to travel uphill to the grocery store=
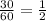
We know, Distance=
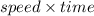
∴ Distance of home to grocery store=
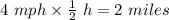
Now, finding the time taken to travel back home.
Time=
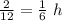
Next,
Total distance travel by Nadia=
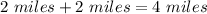
Total time taken travel uphil and downhill=
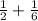
taking LCD
∴ Total time taken travel uphil and downhill=
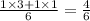
Total time taken travel uphil and downhill=
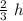
Average speed of entire trip of Nadia=
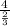
Multiplying the inverse.
∴ Average speed of entire trip of Nadia=
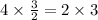
Hence, Average speed of entire trip of Nadia is 6mph.