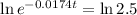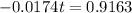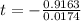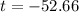Answer:
The solution is
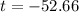
Explanation:
The first step to solve this equation is placing everything with the exponential to one side of the equality, and everything without the exponential to the other side. So
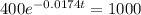
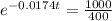
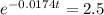
The ln is the interse operation to the exponential, so we apply the ln to both sides of the equality.