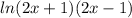Question

Condensing Logarithmic Expression In Exercise,use the properties of logarithms to rewrite the expression as the logarithm of a single quantity.See example 4.

In(2x + 1) + In(2x - 1)

Answer 1

We can use the product rule [
`\text{ln(xy)}=\text{ln(x)~+~\text{ln(y)}}` ] to simplify.

`\text{ln(2x + 1)~+~ln(2x - 1)}`

`\text{ln(2x + 1)(2x - 1)}`

→
`\text{ln}(4\text{x}^2-1})` ←

Best of Luck!

Answer 2

`ln (2x + 1)(2x - 1)`

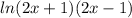
Explanation:

In(2x + 1) + In(2x - 1)

if we have plus inbetween two log terms then we multiply the log terms

the property of log is same as the property of ln

`ln(2x + 1) + ln(2x - 1)`

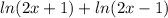
ln m + ln n = ln(mn)

`ln (2x + 1)(2x - 1)`

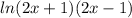
we expressed the give expression as the log of a single quantity

`ln (2x + 1)(2x - 1)`