Question

Inverse Function In Exercise,analytically show that the functions are inverse functions.Then use the graphing utility to show this graphically.

f(x) = e^x/3
g(x) = Inx^3

Answer 1

`g^(-1)(x)=f(x)=e^{(x)/(3)}`

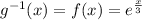
Explanation:

We have been given two functions as
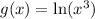`g(x)=\text{ln}(x^3)` and
`f(x)=e^{(x)/(3)}`. We are asked to show that both functions are inverse of each other algebraically and graphically.

Let us find inverse function of
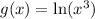`g(x)=\text{ln}(x^3)` as:

`y=\text{ln}(x^3)`

Interchange x and y values:

`x=\text{ln}(y^3)`

Using log property
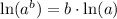`\text{ln}(a^b)=b\cdot \text{ln}(a)`, we will get:

`x=3\cdot \text{ln}(y)`

`(x)/(3)=\frac{3\cdot \text{ln}(y)}{3}`

`(x)/(3)=\text{ln}(y)`

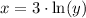
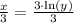
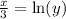
Using log definition; If
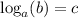`\text{log}_a(b)=c`, then
`b=a^c`, we will get:

`y=e^{(x)/(3)}`

`g^(-1)(x)=e^{(x)/(3)}`

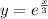
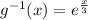
Therefore, we can see that function
`f(x)=e^{(x)/(3)}` is inverse of function
`g(x)=\text{ln}(x^3)`.

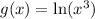We can see that both functions are symmetric about line
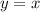`y=x`, therefore, both functions are inverse of each other.