Answer:
The function
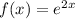 is the inverse of the function
is the inverse of the function

Explanation:
To find the inverse function, swap x and y, and solve the resulting equation for x.
So, for the function
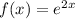 swap the variables:
swap the variables:
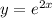 becomes
becomes
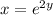
Now, solve the equation
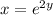 for y.
for y.
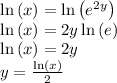
For the function
 swap the variables:
swap the variables:
 becomes
becomes
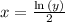
Now, solve the equation
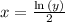 for y.
for y.
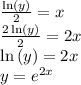
Therefore, the function
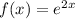 is the inverse of the function
is the inverse of the function

Here is the graph of the function and inverse. We can see that the graph of the inverse is a reflection of the actual function about the line y = x. This will always be the case with the graphs of a function and its inverse.