Question

The concentration C (in mg/dl), of an antibiotic in a patient’s bloodstream per hour, t, is given by: c(t) = (50t)/(t^2+25) In order for the antibiotic to be effective, 4 or more mg/dl must be present in the bloodstream. When do you have to take the antibiotic after the initial dose? Solve algebraically and graphically.

Answer 1

Explanation:

Functions

The problem describes a function that expresses the concentration of an antibiotic in mg/dl vs time in hours as:

`\displaystyle c(t)=(50\ t)/(t^2+25)`

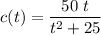
We need to find the first value of t such that

`\displaystyle c(t)\geq 4`

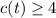
It means that

`\displaystyle (50\ t)/(t^2+25)\geq 4`

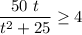
Operating with the inequality

`\displaystyle 50\ t\geq 4\ t^2+100`

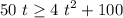
Rearranging and dividing by 2, we have a polynomial inequality:

`\displaystyle 2t^2-25t+50\leq 0`

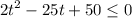
Factoring

`\displaystyle 2(t-10)\left (t-(5)/(2)\right )\leq 0`

There are two possible values for t, both valids because they are positive

`\displaystyle t=(5)/(2)=2.5, \ t=10`

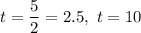
We need to find the first value, i.e.

`t=2.5 \ hours`

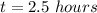
Now for the graphic method, we plot the graph for the function and a horizontal line at c=4 to find the values of t.

The graph is shown in the image provided below. We can see both values where the funcion and C=4 intersect. Both values coincide with the previously analitically found values