Answer:
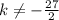
Explanation:
We have been given a system of equations as
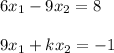 . We are asked to find the value of k such that the given system is consistent.
. We are asked to find the value of k such that the given system is consistent.
Let us consider two equations as:
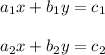
For a system to be consistent the ratio of coefficient of x terms and y terms should not be equal that is:
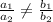
Upon substituting our given values, we will get:


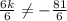
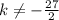
Since the given system will be consistent for all value except
 , therefore, we can choose any values for k such as
, therefore, we can choose any values for k such as
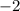 or 2.
or 2.