Answer:
Convergent;
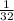 .
.
Explanation:
We have been given an integral as
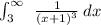 . We are asked to determine whether our given integral converges or diverges.
. We are asked to determine whether our given integral converges or diverges.
Let us integrate our given integral by u substitution as:
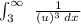
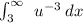
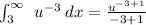
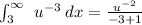
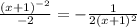
Now, we will compute the boundaries.
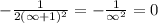
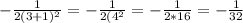
Our definite integral would be
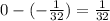
Therefore, our given integral is convergent and its value is
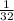 .
.