Answer:
a)
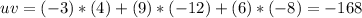
Since the dot product is not equal to zero then the two vectors are not orthogonal.
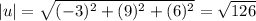
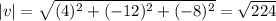
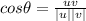
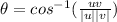
If we replace we got:
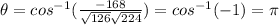
Since the angle between the two vectors is 180 degrees we can conclude that are parallel
b)
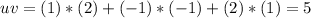
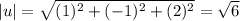
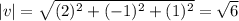
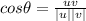
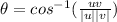
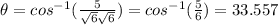
Since the angle between the two vectors is not 0 or 180 degrees we can conclude that are either.
c)
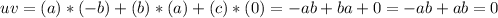
Since the dot product is equal to zero then the two vectors are orthogonal.
Explanation:
For each case first we need to calculate the dot product of the vectors, and after this if the dot product is not equal to 0 we can calculate the angle between the two vectors in order to see if there are parallel or not.
Part a
u=[-3,9,6], v=[4,-12,-8,]
The dot product on this case is:
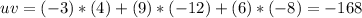
Since the dot product is not equal to zero then the two vectors are not orthogonal.
Now we can calculate the magnitude of each vector like this:
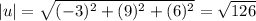
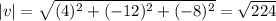
And finally we can calculate the angle between the vectors like this:
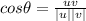
And the angle is given by:
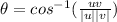
If we replace we got:
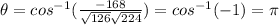
Since the angle between the two vectors is 180 degrees we can conclude that are parallel
Part b
u=[1,-1,2] v=[2,-1,1]
The dot product on this case is:
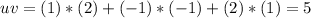
Since the dot product is not equal to zero then the two vectors are not orthogonal.
Now we can calculate the magnitude of each vector like this:
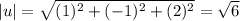
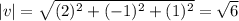
And finally we can calculate the angle between the vectors like this:
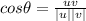
And the angle is given by:
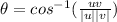
If we replace we got:
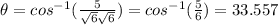
Since the angle between the two vectors is not 0 or 180 degrees we can conclude that are either.
Part c
u=[a,b,c] v=[-b,a,0]
The dot product on this case is:
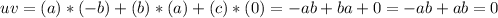
Since the dot product is equal to zero then the two vectors are orthogonal.